Introduction: A Simple EVAL and COMPILE Example
This article is part-01 of the series A Quick Taste of Programming Languages in my blog.
The series is tend to discuss some basic concepts in PL theory and their implementation from a beginner’s perspective. I use Scala code for demonstrations since I’m currently learning it.
The full list of code in this article can be found here. It’s released under the MIT license.
So… What am I doing here? #
Programming language is an attractive and somehow mysterious topic with a long tradition in the field of computer science. I am not going to introduce its history or evolution right now because I’m just a newcomer in this area (it’s the famous SICP course I studied recently that brought me here). But I can assure you that learning the theory of programming languages and compilation is an exciting and mind-refreshing journey, especially when you already have some programming experience.
It’s far beyond my knowledge and ability to offer a systematic course. So I regard my articles as some sort of “supplements” to those who are interested in this field. After clarifying this, it’s time for us to start!
Some concepts #
In essence, the role of programming languages is to define a computational model, enabling programmers to describe their problems. In a computational model, once the “describing” process is correctly done, the answer always comes automatically (though it may be inefficient). But of course, life is not that easy. Writing the description of your problem with pen and paper won’t give you the answer. This is why we need computer, which takes your description and performs calculation on behalf of you, to obtain the answer.
Another aspect should be notice is that there are huge difference between computational models. The computational model defined by Python looks have little to do with the one that defined by RISC-V ISA. Some models offer a strong ability in abstracting your problems, while some others have high affinity to machines instead of humans. There are two ideas to bridge such gaps. The first idea is to translate the models, usually from higher level to lower level (we refer to the one that is more closely to human as “higher level”). This is what we called “compilation”. The other idea is using models in one level to implement a virtual machine, which is able to read and execute models in another level. This is usually refer to as “interpretation” (lower model executes higher model) or “simulation” (higher model executes lower model).
In this introduction article, we will define three different languages, from a human-readable style to a stack machine type style, to illustrate how to evaluate expressions in a language, and how to do transformation between languages. Though this example is rather simple, it should give you a basic impression on what you will deal with when studying PL.
A “higher level” language #
Open a book about compilation principles, you will always find chapters like “lexing” and “parsing” in the beginning part of it. Lexing and parsing are the analyzing steps to transform the strings you write (that is, the “program”) into data structures in the compiler. These structures are called “intermediate representation”, or “IR”. In our adventure, we will skip the analyzing process to directly start with IR, because lexing and parsing are somehow tedious and are not interesting topics nowadays.
Here I’m giving the definition of an IR, which is also the abstract syntax definition of a simple language:
abstract class hIR_Expr
case class hIR_Number(n: Int) extends hIR_Expr
case class hIR_Sum(e1: hIR_Expr, e2: hIR_Expr) extends hIR_Expr
case class hIR_Mul(e1: hIR_Expr, e2: hIR_Expr) extends hIR_Expr
case class hIR_Val(name: String) extends hIR_Expr
case class hIR_Let(name: String, e1: hIR_Expr, e2: hIR_Expr) extends hIR_Expr
All the elements here belong to Expr (expression). There are five types of elements in this language: Number takes an integer, Sum and Mul take two Exprs, Val takes a string and Let takes a string and two Exprs. Programs in this language form recursive trees.
We are using abstract syntax, because we don’t care how the concrete syntax is defined. Maybe the rules order you to write something like (sum 1 2) or (1 sum 2), but after lexing and parsing, they will all become hIR_Sum(hIR_Number(1), hIR_Number(2)).
At present we only know how to construct elements in this language, but it seems not enough because we don’t know its semantics, which specifies the meaning of these elements and how are they functioning. There is a mathematical way to define semantics formally, but since this language is easy for you to understand and it’s hard for me to write the definitions, I will simply give you the evaluator (interpreter) of this language, which can also illustrate its semantics.
type hIR_Env = List[(String, Int)]
def hIR_Eval(e: hIR_Expr, env: hIR_Env = Nil): Int = {
def assoc(name: String, env: hIR_Env): Int = env match{
case Nil => throw new RuntimeException("Val not found.")
case _ => if env.head._1 == name then env.head._2 else assoc(name, env.tail)
}
e match
case hIR_Number(n) => n
case hIR_Sum(e1, e2) => hIR_Eval(e1, env) + hIR_Eval(e2, env)
case hIR_Mul(e1, e2) => hIR_Eval(e1, env) * hIR_Eval(e2, env)
case hIR_Val(name) => assoc(name, env)
case hIR_Let(name, e1, e2) => hIR_Eval(e2, (name, hIR_Eval(e1, env)) :: env)
}
The evaluator takes an expression and an environment, and returns an integer as the result of the input expression. It recursively pattern matching through the expression tree. The environment is a list of pairs of names and their values.
When a Val is encountered, the evaluator will search the environment list and return the first value appears in the list that associates with the Val’s name. When a Let is encountered, the evaluator will first evaluate e1, combines it with name, updates env by adding name and its value, and then evaluates e2 under the updated environment as result.
Notice that duplicate name, such as (let(x, let(x, 1, x + 1), x * x)) won’t cause trouble in this model, because the new name will shade the old one in the environment.
A “lower level” language #
Looks like the language we defined in last section works fine. As a computational model, it enables you to deal with sums and multiplications on integers and their combinations. It also offers a little abstraction abilities: allowing you to give expressions names and using them. Is there any dissatisfaction?
Well, some may argue that this language requires its evaluator to maintain the name-value pairs, which is not very efficient. There must be a way to remove these names in runtime. According to this demand, a lower level language is put forward:
abstract class lIR_Expr
case class lIR_Number(n: Int) extends lIR_Expr
case class lIR_Sum(e1: lIR_Expr, e2: lIR_Expr) extends lIR_Expr
case class lIR_Mul(e1: lIR_Expr, e2: lIR_Expr) extends lIR_Expr
case class lIR_Val(nth: Int) extends lIR_Expr
case class lIR_Let(e1: lIR_Expr, e2: lIR_Expr) extends lIR_Expr
And this is its evaluator:
type lIR_Env = List[Int]
def lIR_Eval(e: lIR_Expr, env: lIR_Env = Nil): Int = e match {
case lIR_Number(n) => n
case lIR_Sum(e1, e2) => lIR_Eval(e1, env) + lIR_Eval(e2, env)
case lIR_Mul(e1, e2) => lIR_Eval(e1, env) * lIR_Eval(e2, env)
case lIR_Val(nth) => env(nth)
case lIR_Let(e1, e2) => lIR_Eval(e2, lIR_Eval(e1, env) :: env)
}
This new language looks very similar to the higher level one, except it doesn’t mark Vals as strings, but only gives it its index in the environment. The environment is also simplified into a list of integers. Below is a picture comparing these two languages, with the env at each evaluator call marked in orange.

Clearly, the lower level language has a better runtime performance, but it will be painful writing programs in this language, because you have to deduce the state of the environment in order to refer to a val correctly.
Now, a brilliant idea naturally comes into our mind: why not coding in the higher level language and then transform the code into the lower level one before we run it? Cool, that’s what people did in the past 50 years!
To achieve this, we need to implement a compiler, which takes an Expr in the higher level language as input and returns an Expr in the lower level language as output:
type h2l_Env = List[String]
def h2l_compiler(e: hIR_Expr, env: h2l_Env = Nil): lIR_Expr = e match {
case hIR_Number(n) => lIR_Number(n)
case hIR_Sum(e1, e2) => lIR_Sum(h2l_compiler(e1, env), h2l_compiler(e2, env))
case hIR_Mul(e1, e2) => lIR_Mul(h2l_compiler(e1, env), h2l_compiler(e2, env))
case hIR_Val(name) => lIR_Val(env.indexOf(name))
case hIR_Let(name, e1, e2) => lIR_Let(h2l_compiler(e1, env), h2l_compiler(e2, name :: env))
}
The compilation process is pretty straight forward since these two languages are very similar. The only tricky part is the compiler should using a list of strings to track the index of names in the higher level language, and passing this information to the lower one.
A “stack machine level” language #
What we have done so far is good, but a further step is needed if we want to bridge our code to a real world machine.
We can treat the evaluators we have implemented as some sort of “virtual machines”, but they implicitly inherits the power of Scala. Specifically speaking, these recursive functions rely on a calling stack offered by Scala.
To reveal the details which were hidden before, we can define a language that analogs the behavior of a stack machine.
abstract class smIR_Instr
case class smIR_Const(n: Int) extends smIR_Instr
case class smIR_Sum() extends smIR_Instr
case class smIR_Mul() extends smIR_Instr
case class smIR_Val(nth: Int) extends smIR_Instr
case class smIR_Pop() extends smIR_Instr
case class smIR_Swap() extends smIR_Instr
You can imagine our stack machine as “a CPU + a stack (memory)”, which can be easily implemented in real world. It runs linear instructions one by one, takes data from the stack and pushes them back after some operation. As you can tell, stack machine language is no longer recursive.
Here is a “simulator” of this stack machine, which helps to show the semantics of these instructions. Notice that this is a tail recursive function.
type stack = List[Int]
type insts = List[smIR_Instr]
def sm_simulator(ins: insts, stk: stack = Nil): stack = ins match {
case Nil => stk
case _ => ins.head match {
case smIR_Const(n) => sm_simulator(ins.tail, n :: stk)
case smIR_Sum() => sm_simulator(ins.tail, (stk(0) + stk (1)) :: stk.drop(2))
case smIR_Mul() => sm_simulator(ins.tail, (stk(0) * stk (1)) :: stk.drop(2))
case smIR_Val(nth) => sm_simulator(ins.tail, stk(nth) :: stk)
case smIR_Pop() => sm_simulator(ins.tail, stk.drop(1))
case smIR_Swap() => sm_simulator(ins.tail, List(stk(1), stk(0)) ::: stk.drop(2))
}
}
Const(n): push integernto the stack.Sum: pop the top two elements on the stack and pushes back their sum.Mul: pop the top two elements on the stack and pushes back their product.Val(n): push the integer that equals thenth element counting from top to the stack.Pop: pop the top element on the stack.Swap: swap the top two elements on the stack.
After defining the stack machine language, we can implement a compiler to transform the “lower level” language to the stack machine language. The implementation may be easier than you would expect:
type insts = List[smIR_Instr]
type depth = List[Int]
def l2sm_compiler(e: lIR_Expr, d: depth = Nil): insts = {
def update(d:depth): depth = d.map(i => i + 1)
e match
case lIR_Number(n) => List(smIR_Const(n))
case lIR_Sum(e1, e2) => l2sm_compiler(e1, d) ::: l2sm_compiler(e2, update(d)) ::: List(smIR_Sum())
case lIR_Mul(e1, e2) => l2sm_compiler(e1, d) ::: l2sm_compiler(e2, update(d)) ::: List(smIR_Mul())
case lIR_Val(nth) => List(smIR_Val(nth + d(nth)))
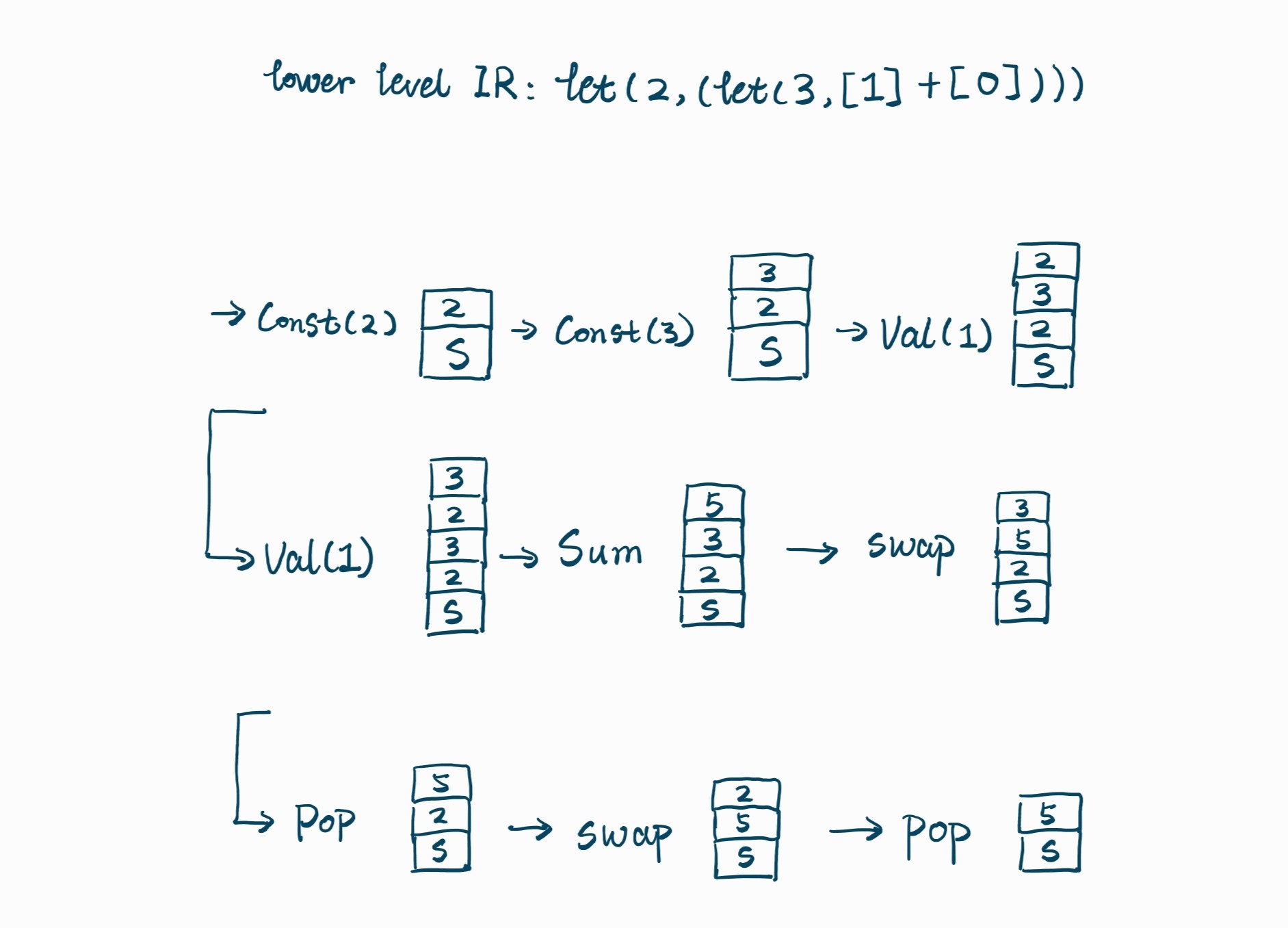
case lIR_Let(e1, e2) => l2sm_compiler(e1, d) ::: l2sm_compiler(e2, 0 :: d) ::: List(smIR_Swap(), smIR_Pop())
}
The compiler needs to maintain the numbers of elements that placed on top Vals in order to find these Vals later. Another interesting part is the compiler should insert Swap + Pop operations to remove the unneeded Vals, because we have to ensure that every Expr in the “lower level” language only leaves its value on top of the stack and doesn’t modify any other things. Below is a picture showing this process.
Summary #
So much for this example. In this article we explored some basic ideas in programming languages and conducted some hands-on. If you want to play with the code, I recommend you to run it on a online Scala interpreter (in case you don’t have Scala interpreter installed on your PC).
That’s all. Thanks for reading!